= 23
Add
= 4 - 3
= 1
Multiply
Subtract
= 30 - 16
= 14
Multiply
Subtract
= 5(20) - 9
= 100 - 9
= 91
Evaluate exponent
Multiply
Subtract
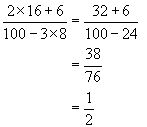
Add and subtract
Simplify fraction
![]()
How much is 3 + 4 x 5? Some beginning
algebra students will say 35 while others will say 23. Since a numerical
expression can have only one value, only one of these
answers can be correct.
To avoid confusion (and even conflict)
mathematicians long ago agreed on a convention called the Order
of Operations.
The Order of Operations tells us how to evaluate an
expression in the correct order:
1. Simplify all expressions inside Parentheses, brackets, braces, etc.
2. Evaluate all Exponents.
3. Multiply and Divide left to right.
4. Add and Subtract left to right.
5.
Simplify fractions.
Many students use the mnemonic PEMDAS
(Please
Excuse My Dear Aunt Sally)
to remember the order of operations.
The solution to the problem above is
23 as shown below in example 1.
Examples:
| 1.3 + 4 x 5 | 3
+ 4 x 5 = 3 + 20
= 23 |
Multiply
Add |
| 2.
|
= 4 - 3 = 1 |
Divide
(left to right!)
Multiply Subtract |
|
3.
3(3
+ 7) - 16
|
3(3
+ 7) - 16 = 3(10) - 16
= 30 - 16 = 14 |
Add
inside parenthesis
Multiply Subtract |
|
4.
5(13
+ 7) - (7 - 4)2
|
5(13
+ 7) - (7 - 4)2 = 5(20) - 32
= 5(20) - 9 = 100 - 9 = 91 |
Simplify
parentheses
Evaluate exponent Multiply Subtract |
| 5. |
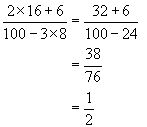 |
Multiply top and bottom
Add and subtract Simplify fraction
|
| 6. Place parentheses in
the following problem in order for it to be correct:
|
If you place parentheses around the 7 - 4, then apply the order of operations, you will have a true equation. | |