The following properties are true for any real numbers a, b, and c.
 

I. The Computational Properties:  Commutative, Associative, Distributive, Identity.

 

1. The Commutative Property of Addition.  "Commutative " means that something moves back and forth, as in "commuting" to work.  The commutative property of addition allows the order of addition to be changed. 3 + 5 = 5 + 3 We know that both expressions equal 8.   In more formal language,   If a and b are two real numbers,  then a + b = b + a.

2. The Commutative Property of Multiplication. The commutative property of multiplication allows the order of addition to be changed.

3 × 5 = 5 × 3

We know that both expressions equal 15.

In more formal language,

If a and b are two real numbers, then ab = ba.

 

3.  The Associative Property of Addition. "Associative" refers to association or grouping.  In arithmetic, grouping is done with parentheses.  So, this property allows that under certain circumstances, that is, in a series of terms that are being added, grouping can be changed. (3 + 5) + 7 = 3 + (5 + 7)

In more formal language,

If a, b,  and c are three real numbers, then (a + b) + c = a + (b + c).

4. The Associative Property of Multiplication. This property allows that in a series of terms that are being multiplied, grouping can be changed.

(3 × 5) × 7 = 3 × (5 × 7)

 

In more formal language,

 

If a, b,  and c are three real numbers, then (ab)c = a(bc).

5.  The Distributive Property.  This may be the most important of the properties because it leads to our notions of "combining like terms" and "factoring." 

If a, b,  and c are three real numbers, then

a(b + c) = ab + bc  and  (b + c)a = ba + ca

also,

a(b – c) = ab – bc  and  (b – c)a = ba – ca

Because a, b, and c, are real numbers, they can be variables or specific numbers and the property holds true.

6. Identity Properties. Identities are numbers that when used in an operation give an answer that is identical to what we started with.

Addition has as its identity element the number zero because any number a added with zero gives a as the result:

a + 0 = a

This is the Identity Property of Addition.

 

Multiplication has as its identity element the number one because any number a multiplied with one gives a as the result:
 

a ·1 = a

 This is the Identity Property of Multiplication.
 

7.  The Multiplicative Property of Zero. Any number a multiplied with zero give zero as its result.

a ·0 = 0 ·a = 0

This property is important because we use it to solve equations that can be factored.
 

8. The Substitution Property. If a = b, then a may be substituted for b and vice versa.

This is, perhaps, the most used property in all of mathematics.  We use whenever we evaluate an expression or perform an operation.
 

II.  The Properties of Equality and Inequality.

1. The Reflexive Property.  If a is a real number, then a = a.  This may seem obvious (and it should!), but this statement is important because it means that each number can have only one value (although that value can be expressed in different ways).  If a = 1/2, then a cannot have any other value!  It cannot also equal 3 or -6.7 or something else.  Note, a can be expressed as 0.5, for that has the same value (or amount) as 1/2.

2. The Symmetric Property. If a and b are two real numbers and a = b, then b = a.  This says that we can turn an equation around and the equation is still the same.

 3.  The Transitive Property. If a, b, and c are real numbers, and further, if a = b and b = c, then a = c.  This is a consequence of the substitution property (can you see why?).
 

The following five properties lie at the heart of our equation solving techniques.
 

4.  The Addition Property of Equality. If a, b, and c are real numbers, and a = b, then a + c = b + c.  The idea is this:  if two quantities are equal (as in the case of a balance beam with equal weights on it), then adding the same to both sides keeps things equal.

 

5.  The Subtraction Property of Equality. If a, b, and c are real numbers, and a = b, then a – c = b – c.  The idea is this:  if two quantities are equal (as in the case of a balance beam with equal weights on it), then subtracting the same to both sides keeps things equal.

 

6.  The Multiplication Property of Equality. If a, b, and c are real numbers, and a = b, then a × c = b × c.  The idea is this:  if two quantities are equal (as in the case of a balance beam with equal weights on it), then multiplying both sides by the same amount keeps things equal.

7.  The Division Property of Equality. If a, b, and c are real numbers, and a = b, then a ÷ c = b ÷ c.  The idea is this:  if two quantities are equal (as in the case of a balance beam with equal weights on it), then dividing both sides by the same amount keeps things equal.

8.  The Function Property of Equality. If a, and b are real numbers, and a = b, then f(a) = f(b) provided the function is defined for both a and b.  This is not an official algebraic property, but it embodies the idea that "what we do on one side of the equation, we must do on the other side of the equation to maintain equality.  This is the core of how we solve problems like x ³ = 125: we take the cube root of both sides.
 

III.  The Closure Property and the System of Real Numbers.

1. If any two numbers in a set are operated on by some operation, and the result is always a number in that set, then the set is said to be closed under that operation.  This is called the Closure Property.

This means that if we study an operation, say addition, then if we add any two numbers from a larger set of numbers, say, the integers, and the answer itself is always an integer, then we say that the integers are closed under the operation of addition. Note:  this property is about sets of numbers as much as it is about operations.

2. Number Sets
 

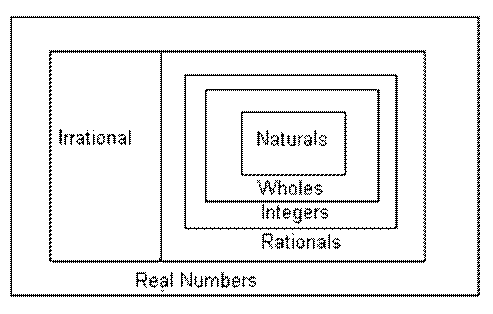
This diagram illustrates the relationships between the sets of numbers in the Real Number System.  It is important to know that a Whole Number, for example, is also an Integer and is also a Rational Number and a Real Number at the same time!  Thus, the rectangles above show that numbers that are in a certain subset of the real numbers are automatically in other subsets at the same time.

a. The Natural numbers are the “counting numbers”, that is 1, 2, 3, 4, …

b. The Whole numbers are the Natural numbers plus the element 0.  They are 0, 1, 2, 3, …

c. The Integers are defined as any rational number whose denominator is 1.  They are …, -2, -1, 0, 1, 2, …  When we draw number lines, we usually label the integers.

d. The Rational numbers are any numbers that can be written as a fraction of two integers.  Examples are -3/4, 0.35, 5, and 1,000.

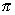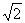e. The Irrational numbers are any numbers that cannot be written as a fraction of two integers.  The most famous example is .  Other examples are  and e = 2.718281828…  Any square root of a number that is not a perfect square is irrational.  Similarly, any cube root of a number that is not a perfect cube is irrational (and so on).

f. No number is both Irrational and Rational at the same time.

g. The Real numbers are all of the Rationals and all of the Irrationals taken together.  Every real number is either rational or irrational.  The number line is a picture of the entire real number system.
 

3.  Examples.

The Integers are closed under the operation of addition because every time you add two integers, the result is an integer.

The Whole numbers are closed under the operation of multiplication because every time you multiply two whole numbers, the result is a whole number.

The Natural numbers are not closed under the operation of subtraction.  A counterexample is 4 – 9 = -5.  We subtracted 9 from 4 (both are natural numbers) and the result was -5 which is not a natural number.