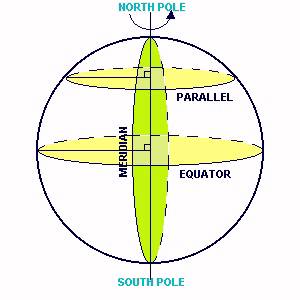
To see how some spherical geometry can be used, let's look at an everyday example - the measurement of position and distance on the surface of the Earth. The rotation of the Earth on its axis presents us with an obvious means of defining a coordinate system for the surface of the Earth. The two points where the rotation axis meets the surface of the Earth are known as the north pole and the south pole and the great circle (a circle on the surface of a sphere of which center is pass through the center of the sphere) perpendicular to the rotation axis and lying half-way between the poles is known as the equator. Great circles which pass through the two poles are known as meridians and small circles which lie parallel to the equator are known as parallels.

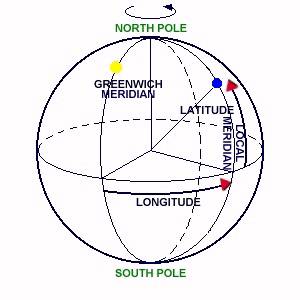
The Longitude of the point is measured east or west along the equator and its value is the angular distance between the local meridian passing through the point and the Greenwich meridian (which passes through the Royal Greenwich Observatory in London). Because the Earth is rotating it is possible to express longitude in time units as well as angular units. The Earth rotates by 360° in 24 hours. Hence, the Earth rotates 15° of longitude in 1 hour, 1° of longitude in 4 minutes, 1' of longitude in 4 seconds and 1" of longitude in 1/15 second.

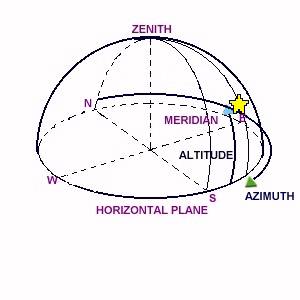
The latitude of a point is the angular distance north or south of the equator, measured along the meridian passing through the point. A related term is the co-latitude, which is defined as the angular distance between a point and the closest pole as measured along the meridian passing through the point. In other words, co-latitude = 90°- latitude.

The horizontal coordinate system (commonly referred to as the alt-az system) is the simplest coordinate system as it is based on the observer's horizon. The celestial hemisphere viewed by an observer on the Earth is shown in figure. The great circle through the zenith and the north celestial pole cuts the horizon at the north point (N) and the south point (S).

The altitude is the angle measured along the vertical circle from the horizon. It is measured in degrees. An often-used alternative to altitude is the zenith distance, z = 90 - a. 

The azimuth may be defined in a number of ways, but generally, defined as the angle between the vertical through the north point and the vertical through the star, measured eastwards from the north point along the horizon from 0° to 360°. This definition applies to observers in both the northern and the southern hemispheres.

 Because the altitude and azimuth of a star are constantly changing, it is not possible to use the horizontal coordinate system in a catalogue of positions. A more convenient coordinate system for cataloguing purposes is one based on the celestial equator and the celestial poles and defined in a similar manner to latitude and longitude on the surface of the Earth. In this system, known as the equatorial coordinate system, the analogue of latitude is the declination.
 

The declination (Dec. or d;) of a star is its angular distance in degrees measured from the celestial equator along the meridian through the star. It is measured north and south of the celestial equator and ranges from 0° at the celestial equator to 90° at the celestial poles, being taken to be positive when north of the celestial equator and negative when south. 
 

As Greenwich meridian has been (arbitrarily) selected as the zero point for the measurement of longitude, the zero point chosen on the celestial sphere is the vernal equinox (spring equinox of the two points where the ecliptic and the celestial equator meet (time of year of equal length of day and night). The angle between it and the intersection of the meridian through a celestial object and the celestial equator is called the right ascension (R.A. or a) and it is measured from 0 h to 24 h along the celestial equator eastwards (counterclockwise) from the first point of Aries (vernal equinox).