Implicit Differentiation
A consequence of the chain rule is the technique of implicit differentiation. An implicit function is one in which y is dependent upon x but in such a way that y may not be easily solved in terms of x. An example of an implicit function that we are familiar with is
![]()
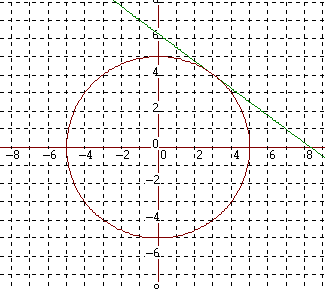
which is the equation of a circle whose center is (0, 0) and whose radius is 5. This would not normally be considered a function since its graph violates the vertical line test. It is possible to solve the equation for y. When we do, we get two equations, which not surprisingly produce the upper and lower parts of the circle when graphed:
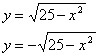
Now, suppose we need to find the equation of the line tangent to the circle at the point (3, 4). This is illustrated below.
|
|
We could differentiate, using the chain rule, the equation for the top of the circle:
![]()
then substitute x = 3 into the formula
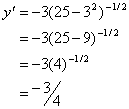
The equation of the tangent line would be
![]() .
.
Implicit differentiation offers a faster way to obtain the derivative. Start with the equation of the circle itself (no solving), then take the derivative of each term:
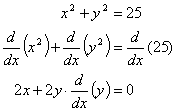
Notice what happens to the y 2 term. We take its derivative in terms of y and multiply by the derivative of y just as the chain rule requires. This derivative of y is normally written y’ (duh!). So, the derivative expression becomes
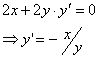
At the point (3, 4), we substitute the values of x and y

The equation of the tangent line is determined as before. You should notice that the two expressions for the derivative y’ are the same expression wherein the second form includes y while the first form has an explicit form of y in terms of x.
The steps for implicit differentiation are typically these:
- Take the derivative of every term in the equation.
- For terms involving y, use the chain rule.
- Solve the resulting formula for y’.
- Use the formula for y’ to solve the problem.
Example.
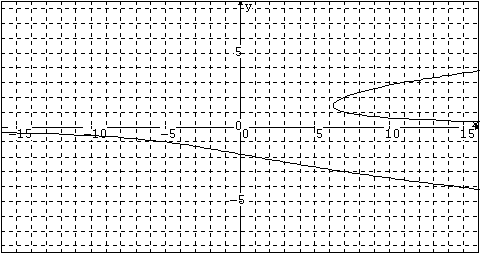
Consider, the implicitly defined function y 3 - xy = -6, which cannot be solved for y (although it can be solved for x). This is not a function in the usual sense. However, the graph (shown below) does have a tangent line and a slope at almost every point. The purpose of implicit differentiation is to be able to find this slope.
|
|
Implicitly differentiate the function:
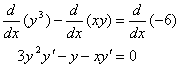
Notice that the product rule was needed for the middle term. The derivative equation is then solved for dy/dx to give
![]()
At the point (7, 2), the tangent line therefore has the slope 2/5. We can also ask at which points do horizontal or vertical tangent lines exist?
For a horizontal tangent line, y’ = 0. This means that y = 0. What is x? Substituting into the original formula gives an impossible result Þ there are no points having a horizontal tangent.
A vertical tangent line has y’ = ¥ Þ 3y 2 - x = 0 Þ x = 3y 2. Since this must also satisfy the original formula, we have
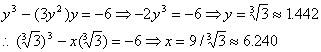
Therefore a vertical tangent occurs at (6.240, 1.442).