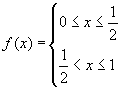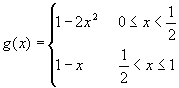The Intermediate Value Theorem states:
 

Suppose f is continuous on a closed interval [a, b]. If k is any number between f(a) and f(b), then there is at least one number c in [a, b] such that f(c) = k.

There is really nothing surprising about this theorem, but its importance is found in an idea called the completeness of the real numbers. This idea asserts that there are no holes or gaps in the real numbers, that they are continuous. 

A frequent use of this theorem is in proving the existence of roots of function.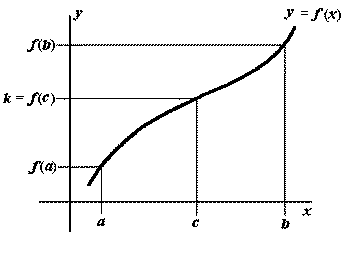 
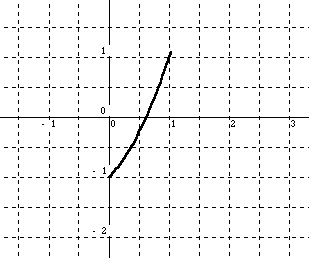
Example: Prove using the ITV that the function 

f(x) = x 2 + x – 1

(shown at right) has a root on the interval [0, 1].
 

Solution: Since f(x) is a polynomial function, it is continuous for all values of x in the interval. Now, the hypothesis of the IVT asserts that there is some value of x = c such that f(c) is between f(0) and f(1).Since f(0) = -1 and f(1) = 1, then there exists a value of x = c such that f(c) = 0.Therefore a root of the function exists on the interval [0, 1].
 

Note that the IVT establishes the existence of the root, but does not establish its value. 

 

Example: Why does the conclusion of the IVT fail on [0, 1] for the following functions?

 

 
Solutions. For the first function, f(x) has only two values, 0 or 1.While it is defined for all x in the closed interval, it is not continuous but is a step function. For the second function, is not defined for all values of x in the interval, rather, it has a hole at x = ½.

 

The graph of f(x).

The graph of g(x)