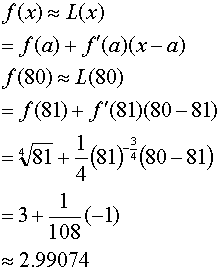Linear Approximations
 
One of the important applications of the derivative at a point is to use it to approximate the value of a function at nearby points.  This works because within a sufficiently small interval around the point, the function can be approximated by a tangent line through the point.
 

 
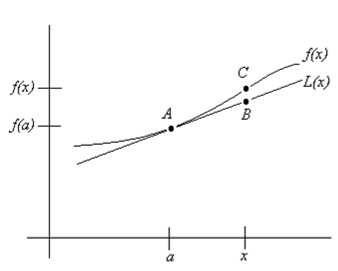
Point A has coordinates (a, f(a)) and is on the curve y = f(x).  A tangent line, L(x) passes through point A.  The slope of this tangent line is the derivative of f(x) at x = a, or f ‘ (a).  Then we can show, using the point-slope form of a line that
 
L(x) = f(a) + f ‘ (a)(x ­– a)

 
If a value of x is sufficiently close to a, then the value of y on the line L(x) will be very close to the value of y on the graph of f(x).  That is, points B and C have almost the same value of y if they have the same value of x.  Therefore, we say that the tangent line L(x) is a linear approximation to the function f(x) for values of x sufficiently close to a.
 
The error, that is f(x) – L(x) depends on x, hence it too is a function of x.  This error function can be written as 
 

 
The percentage error is 
 

 
Some observations about concavity and linear approximations are in order.  First, if the portion of the graph to which we are approximating is concave up (second derivative is positive) as the graph above appears at A, then our line lies below the graph.  Hence, the approximation is an underestimate.  If the graph is concave down (second derivative is negative), the line will lie above the graph and the approximation is an overestimate.

 
Example 1:  Use a linear approximation near x = 3 to estimate the value of f(3.1) if f(x) = x2.
Solution:  Here, a = 3, f(3) = 9, and x = 3.1. Also, for our function, f’(x) = 2x which means that f '(a) =  f '(3) = 6.  Therefore, the equation of the tangent line is 
 

 
Thus we are saying that f(3.1) » 9.6.  How good is this?  Well, substituting into the real function gives f (3.1) = 3.1 2 = 9.61.  The error function is f(x) – L(x) = 0.01

 

 
The percent error is 

 

 
which is pretty good!

 
Example 2.  Another use for the linear approximation is to estimate roots of numbers. Suppose we want to know the fourth root of 80, but do not have a calculator (or the teacher says we can't use one!).  The first thing we might do is wish that the number had been 81. Then we would brilliantly deduce that the answer is 3.  But, alas!  80 is a number close to 81, so we'll use this fact to our advantage.

First, we will define the following function:

 

 
In order to employ a linear approximation, we will need the derivative function (which is why the radical notation is replaced with a power notation).  It is easily shown that

 

 
Then, the linear approximation to f(x) must be

 

 
A comparison of this result with a calculator result shows that our estimate is 0.00004 to large (by nearly a thousandth of a percent!!!).  The fact that our estimate is larger than the real value of f(80) is due to the fact that our function is concave down, which is easily seen from its graph.