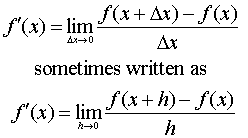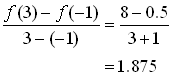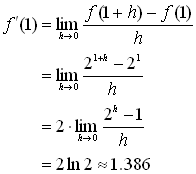The Derivative

The main idea of the derivative is that of rate of change of a function.  In the case of the simplest of functions, the line, this rate of change is its slope.  For non-linear functions, the rate of change is the slope of a secant  line between two points on the graph of the nonlinear function.

In Calculus, we want to describe rates of change in function according to the philosophy of the Rule of Four. We begin with the numerical.

Numerical Approximation. The derivative is the difference quotient applied to two values in a tabulation of function values.  For example, suppose the following table describes the population, in thousands, of a city as a function of time.
 
Year 1998 1999 2000 2001 2002
Pop. 23 25 28 26 25

 
Since we do not know the analytic function that represents the population, we are unable to use an algebraic derivative.  Therefore, we use the difference quotient.

 

 

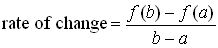Necessarily, the derivative that we calculate is an estimate. Suppose we need to know the derivative of the population function for 2001. The estimated rate of change can be found three ways.

 
1. The rate of change from 2000 to 2001 ("left rate of change") is

 

 

The interpretation of this result is that the population was decreasing at a rate of 2000 people per year in 2001.

 
2. The rate of change from 2001 to 2002 ("right rate of change") is

 

 

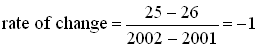The interpretation of this result is that the population was decreasing at a rate of 1000 people per year in 2001.

 
3.  A more believable value for the derivative of the population function for 2001 is obtained if we take the mean of these results. The mean can also be found by finding the rate of change from 2000 to 2002 ("midpoint rate of change"):

 

 

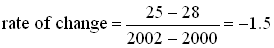The interpretation of this result is that the population was decreasing at a rate of 1500 people per year in 2001.

 
Definition.  The definition of the derivative is the difference quotient in the limit that the distance between the two points over which the rate of change is calculated shrinks to zero. The definition of the derivative is given by

 

 

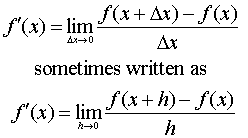
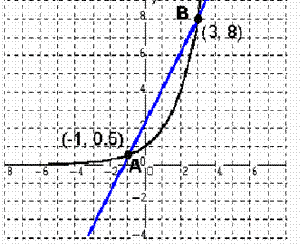
Consider the graph of the function f(x) = 2x shown below. How much is the derivative (rate of change) at the point on the graph where x = 1?

 

 

The slope of the secant line AB approximates the derivative of the function f(x) = 2x at the point (1, 2). The calculation is
 

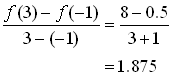
The slope of the tangent line through point A is the derivative (or instantaneous rate of change) of the function f(x) = 2x at the point (1, 2). The calculation is

   
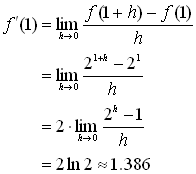
Graphically, the derivative is associated with the slope of a line tangent tangent to a point on the graph of a function (see also Linear Approximations).  This type of rate of change is called an "instantaneous" rate of change because it is not taken between two points, but occurs at one point only. Compare the two graphs above.

We can easily justify this notion by graphing a function, then repeatedly zooming in on the point.  This repeated zooming causes the graph to look linear, a condition that we refer to as "local linearity:" that is, all continuous functions look like lines if we restrict our view to a sufficiently small neighborhood of x. Many students think of this as the "slope" of the curve, an idea that, while technically not "rigorous," can be quite useful and instructive.
 
Analytically.  If the function we are interested in is continuous (no holes, gaps, or jumps) and if it is "smooth" (no corners) over the interval of interest, then the derivative is also a function over that interval.  When these conditions are met, we say the function is differentiable on that interval.  The definition of the derivative, cited above, can be used to find the derivative function.

In principle, the definition can be used to find any derivative.  However, in practice, the algebra can be very labor intensive and inefficient.  Several derivative forms should be easy to derive for a calculus student.  These include the derivative of the power function, the derivative of an exponential function, and the derivatives of sine and cosine.  Using these as a basis and the appropriate limit theorems and the product, quotient, and chain rules of derivatives, essentially any derivative can be analytically determined.

 
Verbally.  The practical meaning of the derivative is important to us when the functions we study involve models of real world phenomena.  Take, for example, a car moving along a highway where the car's distance s(t) from its starting point (that is, s when t = 0) is a function of time.  The derivative of the distance s'(t) = v(t) is the car's velocity.  This velocity is simply the rate of change of the car's position with respect to time. If we view a graph of s(t) versus t, we might see something like that shown below.

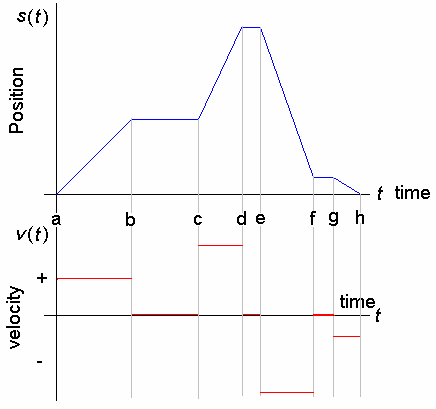At time a, our driver needing to deliver an important report, starts out from home and drives at a constant speed, say 40 mph for 1 hour. This is illustrated by the blue graph on the interval (a, b).  The corresponding red velocity graph (the derivative of the distance traveled) shows a positive velocity of 40 mph. She then stops for lunch for another hour. The blue graph is horizontal, because her distance from home is not changing.  Consequently, her speed is also zero.  After lunch, she gets onto the freeway and travels at 60 mph for another 40 minutes.  By this time, she is 80 miles from home.  The red graph shows the higher speed on the interval (c, d).  She reaches her destination, delivers the report after spending a few minutes explaining its importance to her colleague. At time e, she gets back onto the freeway and drives home at a speed of 70 mph.  Notice that the red graph shows a negative velocity now.  This is because the distance between where she is and home is decreasing.  After 50 minutes of driving, she gets off the freeway so that she can stop at the store for a few groceries.  Again, the blue graph is horizontal, and the red graph is zero on (f, g). She drives the remaining few miles home at 30 mph completing the journey at time h.
 

Important remarks: 

  1. When the function is increasing, the derivative is positive.
  2. When the function is decreasing, the derivative is negative.
  3. When the function is constant, the derivative is zero.
  4. The value of the derivative at any time t or value of x is the rate of change of the function at that t or value of x.
  5. The units of the derivative are the function's vertical units over the function's horizontal units.

 
For algebraic equations, specific rules, or "shortcuts" are employed for finding derivatives for the different family of functions that we study and model with.