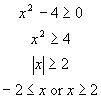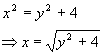A function is a relation between two sets in which each member of the domain produces only one member in the range. Sometimes we refer the domain as input and the range as output. A function can be represented several ways (the Rule of Four).  For example:
 

This is a numerical representation of a function.
 

x … -5 -4 -3 -2 -1 0 1 2 3 4 5 … y … 25 16 9 4 1 0 1 4 9 16 25 …

Analytically, this function is represented by y = x 2.     Graphically, this function is shown at right, the familiar shape known as a parabola.     Verbally, we could write something like, “each output (value in the range) is the result of squaring its input (value in the domain)."
A relation is not a function if a value in the domain produces more than one value in the range.  For example, the table at right. Here x = 0 resulted in two different values of y.  x 0 2 0 3 y 5 7 3 8
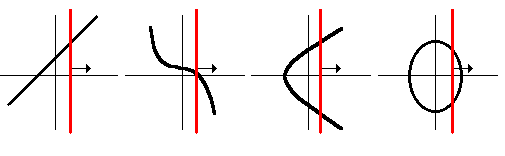
Another way to show whether a relation is a function is by applying the Vertical Line Test to its graph.  The idea is simple:  drag a vertical line from left to right across the graph.  If, at any point, the vertical line intersects the graph more than once, the relation is not a function. Here's why:  Every position of the vertical line represents a value of x.  If the line crosses the graph more than once, there exists more than one value of y associated with that value of x. Therefore, the graph is not that of a function. The first two graphs shown below are graphs of functions, while the second two graphs are not graphs of functions. We could, however, argue that the third graph is a graph of x as a function of y. If so, we would expect some clarifying information at the outset of our study of the problem.  The fourth graph (an ellipse) is considered the graph of a relation involving x and y.

Function notation, introduced by Leonhard Euler (pronounced “Oiler”, rather than “You-ler”) is easy and convenient to use.
 

When we write a function f(x) = x² - 4, we identify x as the independent variable and f(x) or y as the dependent variable.  This means,
 
 

f(x) = x ² simply tells us that there is a function that takes x (whatever it is or means) and does something to it.  This is the left side of the equation.  The right side of the equation is the recipe itself, that is, what has to be done to x in the function.  Here, x is being squared.
 

Another function might be g(x) = 3x ² + 1. Note that not all functions require the letter f.  This says that the input x is first squared, then the result is multiplied by 3, and finally 1 is added.  (Recall the Order of Operations).  This rule is applied no matter what x is, even if x itself is another function (this is called Composition of Functions).
 

Examples:
 

g(5) = 3(5) ² + 1 = 76

g(a) = 3a ² + 1

g(2x) = 3(2x) ² + 1 = 12x ² + 1

g(x - 5) = 3(x - 5) ² + 1 = 3x ² - 30x + 76

g(sin x) = 3(sin x) ² + 1 = 3sin ² x + 1  

[Note the syntax used here:  the exponent comes after the "sin". This is to avoid the possible confusion that might occur if the exponent is placed after the x, which would mean the sine of x squared:  sin (x ² ).]
 

Domain and Range.
 
 

The domain of a function is the set of allowable numbers that may be substituted for x.

Thus, the range is the set of numbers that result as the output of a function when every member of the domain is used as an input.
 

Useful hints for finding domains and ranges:
 

Linear equations, power functions and polynomials always have a domain of all real numbers unless the domain is restricted explicitly in the problem, or implicitly by the context of the problem.  Odd degree linear equations, power functions and polynomials always have a range of all real numbers unless the domain is restricted explicitly in the problem, or implicitly by the context of the problem. Even degree functions will have either a maximum or a minimum point that limits the range of the function.
 

If the domain or range is not all real numbers, then they are restricted by consideration of one of the following:
 
 

Domain:  denominators cannot equal 0  radicands > 0  argument of logs > 0 contextual restrictions

Range:  examine graph over the domain  sin x and cos x are always bounded by ±1  radicals > 0  contextual restrictions

Example: Algebraically, find the domain of 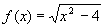.Then, graphically and algebraically, find the range.
 

Solution: This function has a radicand that cannot be negative. So we write
   

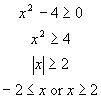
Thus the domain is all real numbers less than -2 and all real numbers greater than 2.
 

Finding the range algebraically means that we are searching for any restrictions on y.  So solve the equation for x:

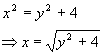
From this we can see that y ² + 4 cannot be negative.  Thus y ² > -4.  Since we are restricted to real numbers, this means that y ² > 0, hence y > 0.
 

 

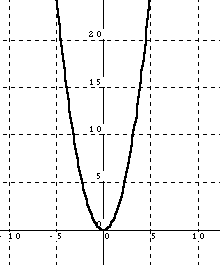
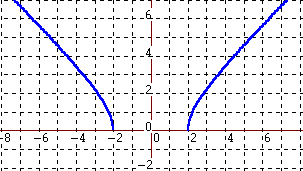
The graph of the function reveals both of these results.  The curve lines up with every point along the x-axis except between -2 and 2 in agreement with our statement about the domain.  The graph lines up with every point along the y-axis from 0 to infinity in agreement with our statement about the range.

Questions?  E-mail me.